Complementary aspects of spatial resolution and signal-to-noise ratio in computational imaging

Abstract

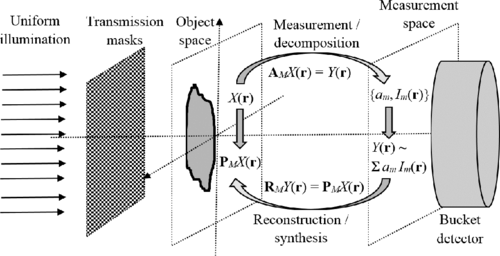
A generic computational imaging setup is considered which assumes sequential illumination of a semitransparent object by an arbitrary set of structured coherent illumination patterns. For each incident illumination pattern, all transmitted light is collected by a photon-counting bucket (single-pixel) detector. The transmission coefficients measured in this way are then used to reconstruct the spatial distribution of the object’s projected transmission. It is demonstrated that the square of the spatial resolution of such a setup is usually equal to the ratio of the image area to the number of linearly independent illumination patterns. If the noise in the measured transmission coefficients is dominated by photon shot noise, then the ratio of the square of the mean signal to the noise variance is proportional to the ratio of the mean number of registered photons to the number of illumination patterns. The signal-to-noise ratio in a reconstructed transmission distribution is always lower if the illumination patterns are nonorthogonal, because of spatial correlations in the measured data. Examples of imaging methods relevant to the presented analysis include conventional imaging with a pixelated detector, computational ghost imaging, compressive sensing, super-resolution imaging, and computed tomography.