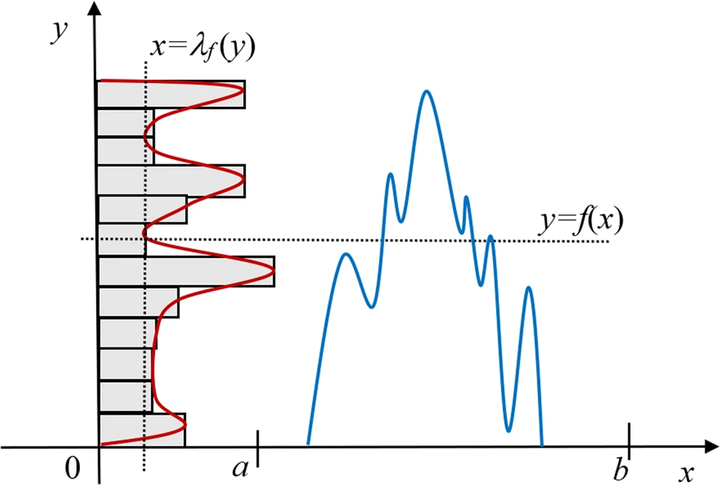
Abstract
We show that the width of an arbitrary function and the width of the distribution of its values cannot be made arbitrarily small simultaneously. In the case of ergodic stochastic processes, an ensuing uncertainty relationship is then demonstrated for the product of correlation length and variance. A closely related uncertainty principle is also established for the average degree of fourth-order coherence and the spatial width of modes of bosonic quantum fields. However, it is shown that, in the case of stochastic and quantum observables, certain non-classical states with sub-Poissonian statistics, such as for example photon number squeezed states in quantum optics, can overcome the “classical” noise-resolution uncertainty limit. This uncertainty relationship, which is fundamentally different from the Heisenberg and related uncertainty principles, can define an upper limit for the information capacity of communication and imaging systems. It is expected to be useful in a variety of problems in classical and quantum optics and imaging.